Back in 2002, Stanford University mathematics professor Robert Osserman chatted with comedian and banjo player extraordinaire Steve Martin in San Francisco’s Herbst Theatre. The event was called “Funny Numbers” and it was intended to deliver an off-kilter discussion on math. Boy did it deliver.
The first half of the discussion was loose and relaxed. Martin talked about his writing, banjos and his childhood interest in math. “In high school, I used to be able to make magic squares,” said Martin. “I like anything kind of ‘jumbly.’ I like anagrams. What else do I like? I like sex.”
Then Robin Williams, that manic ball of energy, showed up. As you can see from the five videos throughout this post, the night quickly spiraled into comic madness.
They riffed on the Osbournes, Henry Kissinger, number theory, and physics. “Schrödinger, pick up your cat,” barks Williams at the end of a particularly inspired tear. “He’s alive. He’s dead. What a pet!”
When Martin and Williams read passages from Martin’s hit play, Picasso at the Lapin AgileWilliams read his part at different points as if he were Marlon Brando, Peter Lorre and Elmer Fudd. At another time, Williams and Martin riffed on the number zero. Williams, for once acting as the straight man, asked Osserman, “I have one quick question, up to the Crusades, the number zero didn’t exist, right? In Western civilization.” To which Martin bellowed, “That is a lie! How dare you imply that the number zero…oh, I think he’s right.”
The videos are weirdly glitchy, though the audio is just fine. And the comedy is completely hilarious and surprisingly thought provoking.
Note: An earlier version of this post appeared on our site in September, 2015.
Jonathan Crow is a Los Angeles-based writer and filmmaker whose work has appeared in Yahoo!, The Hollywood Reporter, and other publications. You can follow him at @jonccrow. And check out his blog Veeptopus, featuring lots of pictures of vice presidents with octopuses on their heads. The Veeptopus store is here.
Ask anyone who’s pursued a career in the sciences what first piqued their interest in what would become their field, and they’ll almost certainly have a story. Gazing at the stars on a camping trip, raising a pet frog, fooling around with computers and their components: an experience sparks a desire for knowledge and understanding, and the pursuit of that desire eventually delivers one to their specific area of specialization.
Or, as they say in science, at least it works that way in theory; the reality usually unrolls less smoothly. On such a journey, just like any other, it might help to have a map.
Enter the work of science writer and physicist Dominic Walliman, whose animated work on the Youtube channel Domain of Science we’ve previously featured here on Open Culture. (See the “Related Content” section below for the links.)
Walliman’s videos astutely explain how the subfields of biology, chemistry, mathematics, physics, and computer science relate to each other, but now he’s turned that same material into infographics readable at a glance: maps, essentially, of the intellectual territory. He’s made these maps, of biology, chemistry, mathematics, physics, and computer science, freely available on his Flickr account: you can view them all on a single page here along with a few more of his infographics..
As much use as Walliman’s maps might be to science-minded youngsters looking for the best way to direct their fascinations into a proper course of study, they also offer a helpful reminder to those farther down the path — especially those who’ve struggled with the blinders of hyperspecialization — of where their work fits in the grand scheme of things. No matter one’s field, scientific or otherwise, one always labors under the threat of losing sight of the forest for the trees. Or the realm of life for the bioinformatics, biophysics, and biomathematics; the whole of mathematics for the number theory, the differential geometry, and the differential equations; the workings of computers for the scheduling, the optimization, and the boolean satisfiability.
Based in Seoul, Colin Marshall writes and broadcasts on cities and culture. His projects include the book The Stateless City: a Walk through 21st-Century Los Angeles and the video series The City in Cinema. Follow him on Twitter at @colinmarshall or on Facebook.
A quick fyi: Dan Kopf, an economics reporter, has a tip that seemed worth passing along. Over at Quartz, he writes:
As a former data scientist, there is no question I get asked more than, “What is the best way to learn statistics?” I always give the same answer: Read An Introduction to Statistical Learning. Then, if you finish that and want more, read The Elements of Statistical Learning. These two books, written by statistics professors at Stanford University, the University of Washington, and the University Southern California, are the most intuitive and relevant books I’ve found on how to do statistics with modern technology… You can download them for free.
If you would like to sign up for Open Culture’s free email newsletter, please find it here. It’s a great way to see our new posts, all bundled in one email, each day.
If you would like to support the mission of Open Culture, consider making a donation to our site. It’s hard to rely 100% on ads, and your contributions will help us continue providing the best free cultural and educational materials to learners everywhere. You can contribute through PayPal, Patreon, and Venmo (@openculture). Thanks!
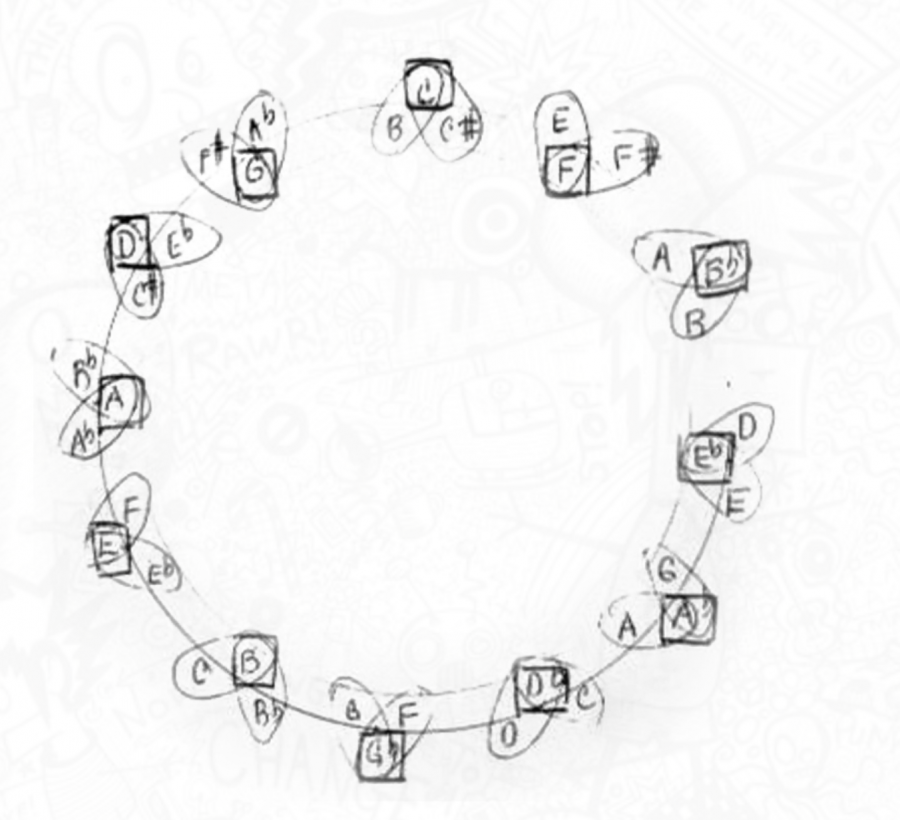
Every musician has some basic sense of how math and music relate conceptually through geometry, in the circular and triadic shapes formed by clusters of notes when grouped together in chords and scales. The connections date back to the work of Pythagoras, and composers who explore and exploit those connections happen upon profound, sometimes mystical, insights. For example, the two-dimensional geometry of music finds near-religious expression in the compositional strategies of John Coltrane, who left behind diagrams of his chromatic modulation that theorists still puzzle over and find inspiring. It will be interesting to see what imaginative composers do with a theory that extends the geometry of music into three—and even four (!)—dimensions.
Pioneering Princeton University music theorist and composer Dmitri Tymoczko has made discoveries that allow us to visualize music in entirely new ways. He began with the insight that two-note chords on the piano could form a Möbius strip, as Princeton Alumni Weekly reported in 2011, a two-dimensional surface extended into three-dimensional space. (See one such Möbius strip diagram above.) “Music is not just something that can be heard, he realized. It has a shape.”
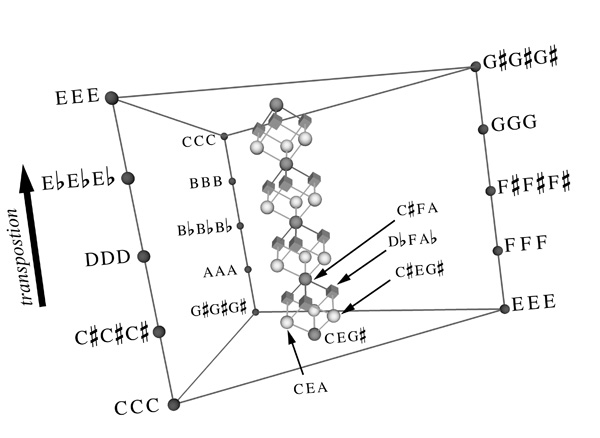
He soon saw that he could transform more complex chords the same way. Three-note chords occupy a twisted three-dimensional space, and four-note chords live in a corresponding but impossible-to-visualize four-dimensional space. In fact, it worked for any number of notes — each chord inhabited a multidimensional space that twisted back on itself in unusual ways — a non-Euclidean space that does not adhere to the classical rules of geometry.
Tymoczko discovered that musical geometry (as Coltrane—and Einstein—had earlier intuited) has a close relationship to physics, when a physicist friend told him the multidimensional spaces he was exploring were called “orbifolds,” which had found some application “in arcane areas of string theory.” These discoveries have “physicalized” music, providing a way to “convert melodies and harmonies into movements in higher dimensional spaces.”
This work has caused “quite a buzz in Anglo-American music-theory circles,” says Princeton music historian Scott Burnham. As Tymoczko puts it in his short report “The Geometry of Musical Chords,” the “orbifold” theory seems to answer a question that occupied music theorists for centuries: “how is it that Western music can satisfy harmonic and contrapuntal constraints at once?” On his website, he outlines his theory of “macroharmonic consistency,” the compositional constraints that make music sound “good.” He also introduces a software application, ChordGeometries 1.1, that creates complex visualizations of musical “orbifolds” like that you see above of Chopin supposedly moving through four-dimensions.
The theorist first published his work in a 2006 issue of Science, then followed up two years later with a paper co-written with Clifton Callendar and Ian Quinn called “Generalized Voice-Leading Spaces” (read a three-page summary here). Finally, he turned his work into a book, A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice, which explores the geometric connections between classical and modernist composition, jazz, and rock. Those connections have never been solely conceptual for Tymoczko. A longtime fan of Coltrane, as well as Talking Heads, Brian Eno, and Stravinsky, he has put his theory into practice in a number of strangely moving compositions of his own, such as The Agony of Modern Music (hear movement one above) and Strawberry Field Theory (movement one below). His compositional work is as novel-sounding as his theoretical work is brilliant: his two Science publications were the first on music theory in the magazine’s 129-year history. It’s well worth paying close attention to where his work, and that of those inspired by it, goes next.
If you would like to sign up for Open Culture’s free email newsletter, please find it here. It’s a great way to see our new posts, all bundled in one email, each day.
If you would like to support the mission of Open Culture, consider making a donation to our site. It’s hard to rely 100% on ads, and your contributions will help us continue providing the best free cultural and educational materials to learners everywhere. You can contribute through PayPal, Patreon, and Venmo (@openculture). Thanks!
Nearly 500 years after his death, we still admire Leonardo da Vinci’s many and varied accomplishments in painting, sculpture, architecture, science, and quite a few other fields besides, most of which would have begun with his putting down some part of the formidable contents of his head on to a piece of paper. (As we’ve seen, sometimes he needed to draw up a to-do list first.) Some of those works remained on paper, and even became famous in that humble form. If you’ve only seen one of Leonardo’s drawings, for instance, it’s almost certainly Vitruvian Man.
Leonardo’s circa-1490 study of the proportions of the human body — or to put it in more common terms, the picture of the naked fellow standing inside a square and a circle — stands at an intersection of art and mathematics, one at which Leonardo spent a great deal of time throughout his life. The Ted-ED lesson above, written by educator James Earle, gets into “the geometric, religious and philosophical significance of this deceptively simple drawing” whose title references the first-century BCE Roman architect and civil engineer Marcus Vitruvius Pollio, who claimed that “the navel is the center of the human body, and that if one takes a compass and places the fixed point on the navel, a circle can be drawn perfectly around the body.”
Vitruvius also realized that “arm span and height have a nearly perfect correspondence in the human body, thus placing the body perfectly inside a square as well.” Both he and Leonardo saw real implications in this alignment between anatomy and geography, beginning with the notion that buildings and other works of man should also take on these “perfect” proportions. All of this ties in with the problem, first proposed by ancient geometers, of “squaring the circle,” that is, finding a procedure to hand-draw a square and a circle both of equal area. Leonardo used Vitruvian Man to point toward one possible solution using the human body.
You can learn more about the importance and legacy of the drawing in the BBC documentary The Beauty of Diagrams, available on Youtube (part one, part two). “Although the diagram doesn’t represent some huge scientific breakthrough,” says its host, mathematician Marcus du Sautoy, “it captures an idea: that mathematics underpins both nature and the manmade world. It represents a synthesis of architecture, anatomy, and geometry. But it’s the perfection and elegance of Leonardo’s solution to this riddle of the square and the circle in Vitruvius which gives the diagram its power and its beauty.” And judging by the unabated popularity of Vitruvian Manparodies, it looks to have at least another half-millennium of relevance ahead.
Based in Seoul, Colin Marshall writes and broadcasts on cities and culture. His projects include the book The Stateless City: a Walk through 21st-Century Los Angeles and the video series The City in Cinema. Follow him on Twitter at @colinmarshall or on Facebook.
In a post earlier this year, we wrote about a drawing John Coltrane gave his friend and mentor Yusef Lateef, who reproduced it in his book Repository of Scales and Melodic Patterns. The strange diagram contains the easily recognizable circle of fifths (or circle of fourths), but it illustrates a much more sophisticated scheme than basic major scale theory. Just exactly what that is, however, remains a mystery. Like every mystical explorer, the work Coltrane left behind asks us to expand our consciousness beyond its narrow boundaries. The diagram may well show a series of “multiplicities,” as saxophonist Ed Jones writes. From the way Coltrane has “grouped certain pitches,” writes vibes player Corey Mwamba, “it’s easy to infer that Coltrane is displaying a form of chromatic modulation.” These observations, however, fail to explain why he would need such a chart. “The diagram,” writes Mwamba, “may have a theoretical basis beyond that.” But does anyone know what that is?
Perhaps Coltrane cleared certain things up with his “corrected” version of the tone circle, above, which Lateef also reprinted. From this—as pianist Matt Ratcliffe found—one can derive Giant Steps, as well as “the Star of David or the Seal of Solomon, very powerful symbolism especially to ancient knowledge and the Afrocentric and eventually cosmic consciousness direction in which Coltrane would ultimately lead on to with A Love Supreme.”
Sound too far out? On the other side of the epistemological spectrum, we have physicist and sax player Stephon Alexander, who writes in his book The Jazz of Physicsthat “the same geometric principle that motivated Einstein’s theory was reflected in Coltrane’s diagram.” Likewise, saxophonist Roel Hollander sees in the tone circle a number of mathematical principles. But, remaining true to Coltrane’s synthesis of spirituality and science, he also reads its geometry according to sacred symbolism.
In a detailed exploration of the math in Coltrane’s music, Hollander writes, “all tonics of the chords used in ‘Giant Steps’ can be found back at the Circle of Fifths/Fourths within 2 of the 4 augmented triads within the octave.” Examining these interlocking shapes shows us a hexagram, or Star of David, with the third triad suggesting a three-dimensional figure, a “star tetrahedron,” adds Hollander, “also known as ‘Merkaba,” which means “light-spirit-body” and represents “the innermost law of the physical world.” Do we actually find such heavy mystical architecture in the Coltrane Circle?—a “’divine light vehicle’ allegedly used by ascended masters to connect with and reach those in tune with the higher realms, the spirit/body surrounded by counter-rotating fields of light (wheels within wheels)”?
As the occult/magical/Kabbalist associations within the circle increase—the numerology, divine geometry, etc.—we can begin to feel like Tarot readers, joining a collection of random symbolic systems together to produce the results we like best. “That the diagram has to do with something,” writes Mwamba, “is not in doubt: what it has to do with a particular song is unclear.” After four posts in which he dissects both versions of the circle and ponders over the pieces, Mwanda still cannot definitively decide. “To ‘have an answer,’” he writes, “is to directly interpret the diagram from your own viewpoint: there’s a chance that what you think is what John Coltrane thought, but there’s every chance that it is not what he thought.” There’s also the possibility no one can think what Coltrane thought.
The circle contains Coltrane’s musical experiments, yet cannot be explained by them; it hints at theoretical physics and the geometry of musical composition, while also making heavy allusion to mystical and religious symbolism. The musical relationships it constructs seem evident to those with a firm grasp of theory; yet its strange intricacies may be puzzled over forever. “Coltrane’s circle,” writes Faena Aleph, is a “mandala,” expressing “precisely what is, at once, both paradoxical and obvious.” Ultimately, Mwamba concludes in his series on the diagram, “it isn’t possible to say that Coltrane used the diagram at all; but exploring it in relation to what he was saying at the time has led to more understanding and appreciation of his music and life.”
The circle, that is, works like a key with which we might unlock some of the mysteries of Coltrane’s later compositions. But we may never fully grasp its true nature and purpose. Whatever they were, Coltrane never said. But he did believe, as he tells Frank Kofsky in the 1966 interview above, in music’s ability to contain all things, spiritual, physical, and otherwise. “Music,” he says, “being an expression of the human heart, or of the human being itself, does express just what is happening. The whole of human experience at that particular time is being expressed.”
When the news broke last week of the death of game-show host Monty Hall, even those of us who couldn’t quite put a face to the name felt the ring of recognition from the name itself. Hall became famous on the long-running game show Let’s Make a Deal, whose best-known segment “Big Deal of the Day” had him commanding his players to choose one of three numbered doors, each of which concealed a prize of unknown desirability. It put not just phrases like “door number three” into the English lexicon but contributed to the world of stumpers the Monty Hall Problem, the brain-teaser based on the much-contested probability behind which door a contestant should choose.
“Behind one door is a car; behind the others, goats,” went the question, setting up a Let’s Make a Deal-like scenario. “You pick a door, say No. 1, and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat. He then says to you, ‘Do you want to pick door No. 2?’ Is it to your advantage to switch your choice?” Yes, replied the unhesitating Savant and her Guinness World Record-setting IQ, you should switch. “The first door has a 1/3 chance of winning, but the second door has a 2/3 chance.”
This logic, which you can see broken down by University of California, Berkeley statistics professor Lisa Goldberg in the Numberphile video at the top of the post, drew about 10,000 letters of disagreement in total, many from academics at respectable institutions. Michael Shermer received a similarly vehement response when he addressed the issue in Scientific American eighteen years later. “At the beginning of the game you have a 1/3rd chance of picking the car and a 2/3rds chance of picking a goat,” he explained. “Switching doors is bad only if you initially chose the car, which happens only 1/3rd of the time. Switching doors is good if you initially chose a goat, which happens 2/3rds of the time.” Thus the odds of winning by switching becomes two out of three, double those of not switching.
Useful advice, presuming you’d prefer a Bricklin SV‑1 or an Opel Manta to a goat, and that the host opens one of the unselected doors every time without fail, which Hall didn’t actually do. When he did open it, he later explained, the contestants made the same assumption many of Savant and Shermer’s complainants did: “They’d think the odds on their door had now gone up to 1 in 2, so they hated to give up the door no matter how much money I offered. By opening that door we were applying pressure.” Ultimately, “if the host is required to open a door all the time and offer you a switch, then you should take the switch. But if he has the choice whether to allow a switch or not, beware. Caveat emptor. It all depends on his mood” — a rare consideration in anything related to mathematics, but when dealing with the Monty Hall problem, one ignores at one’s peril the words of Monty Hall.
Based in Seoul, Colin Marshall writes and broadcasts on cities and culture. His projects include the book The Stateless City: a Walk through 21st-Century Los Angeles and the video series The City in Cinema. Follow him on Twitter at @colinmarshall or on Facebook.
We're hoping to rely on loyal readers, rather than erratic ads. Please click the Donate button and support Open Culture. You can use Paypal, Venmo, Patreon, even Crypto! We thank you!
Open Culture scours the web for the best educational media. We find the free courses and audio books you need, the language lessons & educational videos you want, and plenty of enlightenment in between.
