When I look at maps from centuries ago, I wonder how they could have been of any use. Not only were they filled with mythological monsters and mythological places, but the perspectives mostly served an aesthetic design rather than a practical one. Of course, accuracy was hard to come by without the many mapping tools we take for granted—some of them just in their infancy during the Renaissance, and many more that would have seemed like outlandish magic to nearly everyone in 15th century Europe.
Everyone, it sometimes seems, but Leonardo da Vinci, who anticipated and sometimes steered the direction of futuristic public works technology. None of his flying machines worked, and he could hardly have seen images taken from outer space. But he clearly saw the problem with contemporary maps. The necessity of fixing them led to a 1502 aerial image of Imola, Italy, drawn almost as accurately as if he had been peering at the city through a Google satellite camera.
“Leonardo,” says the narrator of the Vox video above, “needed to show Imola as an ichnographic map,” a term coined by ancient Roman engineer Vitruvius to describe ground plan-style cartography. No streets or buildings are obscured, as they are in the maps drawn from the oblique perspective of a hilltop or mountain. Leonardo undertook the project while employed as Cesare Borgia’s military engineer. “He was charged with helping Borgia become more aware of the town’s layout.” For this visual aid turned cartographic marvel, he drew from the same source that inspired the elegant Vitruvian Man.
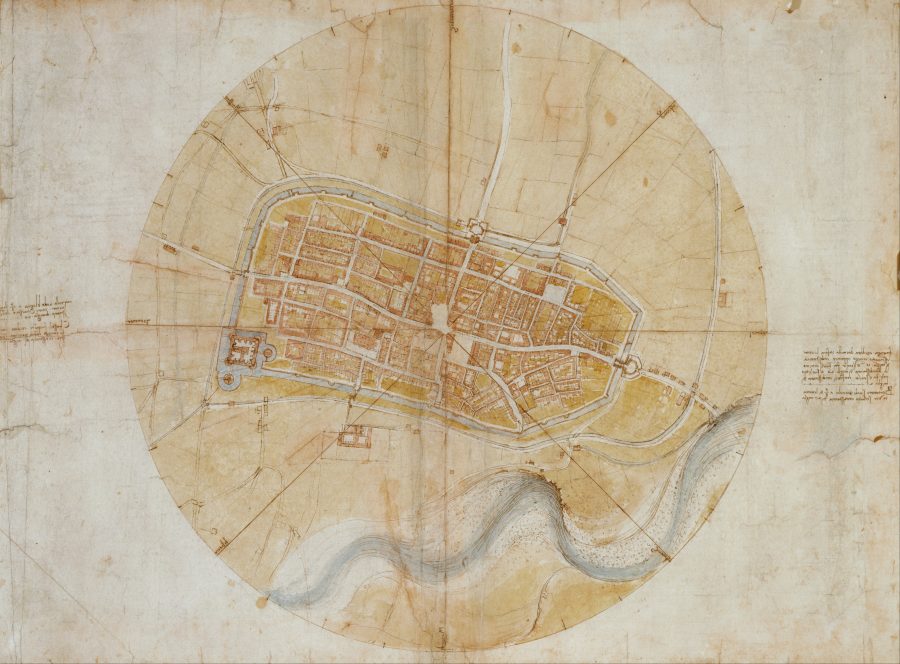
While the visionary Roman builder could imagine a god’s eye view, it took someone with Leonardo’s extraordinary perspicacity and skill to actually draw one, in a startlingly accurate way. Did he do it with grit and moxie? Did he astral project thousands of miles above the city? Was he in contact with ancient aliens? No, he used geometry, and a compass, the same means and instruments that allowed ancient scientists like Eratosthenes to calculate the circumference of the earth, to within 200 miles, over 2000 years ago.
Leonardo probably also used an instrument called a bussola, a device that measures degrees inside a circle—like the one that surrounds his city map. Painstakingly recording the angles of each turn and intersection in the town and measuring their distance from each other would have given him the data he needed to recreate the city as seen from above, using the bussola to maintain proper scale. Other methods would have been involved, all of them commonly available to surveyors, builders, city planners, and cartographers at the time. Leonardo trusted the math, even though he could never verify it, but like the best mapmakers, he also wanted to make something beautiful.
It may be difficult for historians to determine which inaccuracies are due to miscalculation and which to deliberate distortion for some artistic purpose. But license or mistakes aside, Leonardo’s map remains an astonishing feat, marking a seismic shift from the geography of “myth and perception” to one of “information, drawn plainly.” There’s no telling if the archetypal Renaissance man would have liked where this path led, but if he lived in the 21st century, he’d already have his mind trained on ideas that anticipate technology hundreds of years in our future.
Related Content:
Josh Jones is a writer and musician based in Durham, NC. Follow him at @jdmagness