Western Music Moves in Three and Even Four (!) Dimensional Spaces: How the Pioneering Research of Princeton Theorist Dmitri Tymoczko Helps Us Visualize Music in Radical, New Ways

Every musi­cian has some basic sense of how math and music relate con­cep­tu­al­ly through geom­e­try, in the cir­cu­lar and tri­adic shapes formed by clus­ters of notes when grouped togeth­er in chords and scales. The con­nec­tions date back to the work of Pythago­ras, and com­posers who explore and exploit those con­nec­tions hap­pen upon pro­found, some­times mys­ti­cal, insights. For exam­ple, the two-dimen­sion­al geom­e­try of music finds near-reli­gious expres­sion in the com­po­si­tion­al strate­gies of John Coltrane, who left behind dia­grams of his chro­mat­ic mod­u­la­tion that the­o­rists still puz­zle over and find inspir­ing. It will be inter­est­ing to see what imag­i­na­tive com­posers do with a the­o­ry that extends the geom­e­try of music into three—and even four (!)—dimen­sions.

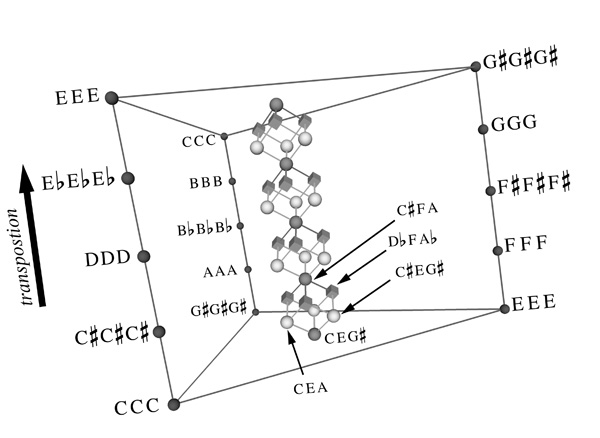
Pio­neer­ing Prince­ton Uni­ver­si­ty music the­o­rist and com­pos­er Dmitri Tymoczko has made dis­cov­er­ies that allow us to visu­al­ize music in entire­ly new ways. He began with the insight that two-note chords on the piano could form a Möbius strip, as Prince­ton Alum­ni Week­ly report­ed in 2011, a two-dimen­sion­al sur­face extend­ed into three-dimen­sion­al space. (See one such Möbius strip dia­gram above.) “Music is not just some­thing that can be heard, he real­ized. It has a shape.”

He soon saw that he could trans­form more com­plex chords the same way. Three-note chords occu­py a twist­ed three-dimen­sion­al space, and four-note chords live in a cor­re­spond­ing but impos­si­ble-to-visu­al­ize four-dimen­sion­al space. In fact, it worked for any num­ber of notes — each chord inhab­it­ed a mul­ti­di­men­sion­al space that twist­ed back on itself in unusu­al ways — a non-Euclid­ean space that does not adhere to the clas­si­cal rules of geom­e­try. 

Tymoczko dis­cov­ered that musi­cal geom­e­try (as Coltrane—and Ein­stein—had ear­li­er intu­it­ed) has a close rela­tion­ship to physics, when a physi­cist friend told him the mul­ti­di­men­sion­al spaces he was explor­ing were called “orb­ifolds,” which had found some appli­ca­tion “in arcane areas of string the­o­ry.” These dis­cov­er­ies have “phys­i­cal­ized” music, pro­vid­ing a way to “con­vert melodies and har­monies into move­ments in high­er dimen­sion­al spaces.”

This work has caused “quite a buzz in Anglo-Amer­i­can music-the­o­ry cir­cles,” says Prince­ton music his­to­ri­an Scott Burn­ham. As Tymoczko puts it in his short report “The Geom­e­try of Musi­cal Chords,” the “orb­ifold” the­o­ry seems to answer a ques­tion that occu­pied music the­o­rists for cen­turies: “how is it that West­ern music can sat­is­fy har­mon­ic and con­tra­pun­tal con­straints at once?” On his web­site, he out­lines his the­o­ry of “macro­har­mon­ic con­sis­ten­cy,” the com­po­si­tion­al con­straints that make music sound “good.” He also intro­duces a soft­ware appli­ca­tion, Chord­Ge­ome­tries 1.1, that cre­ates com­plex visu­al­iza­tions of musi­cal “orb­ifolds” like that you see above of Chopin sup­pos­ed­ly mov­ing through four-dimen­sions.

The the­o­rist first pub­lished his work in a 2006 issue of Sci­ence, then fol­lowed up two years lat­er with a paper co-writ­ten with Clifton Cal­len­dar and Ian Quinn called “Gen­er­al­ized Voice-Lead­ing Spaces” (read a three-page sum­ma­ry here). Final­ly, he turned his work into a book, A Geom­e­try of Music: Har­mo­ny and Coun­ter­point in the Extend­ed Com­mon Prac­tice, which explores the geo­met­ric con­nec­tions between clas­si­cal and mod­ernist com­po­si­tion, jazz, and rock. Those con­nec­tions have nev­er been sole­ly con­cep­tu­al for Tymoczko. A long­time fan of Coltrane, as well as Talk­ing Heads, Bri­an Eno, and Stravin­sky, he has put his the­o­ry into prac­tice in a num­ber of strange­ly mov­ing com­po­si­tions of his own, such as The Agony of Mod­ern Music (hear move­ment one above) and Straw­ber­ry Field The­o­ry (move­ment one below). His com­po­si­tion­al work is as nov­el-sound­ing as his the­o­ret­i­cal work is bril­liant: his two Sci­ence pub­li­ca­tions were the first on music the­o­ry in the magazine’s 129-year his­to­ry. It’s well worth pay­ing close atten­tion to where his work, and that of those inspired by it, goes next.

via Prince­ton Alum­ni Week­ly/@dark_shark

Relat­ed Con­tent:

John Coltrane Draws a Mys­te­ri­ous Dia­gram Illus­trat­ing the Math­e­mat­i­cal & Mys­ti­cal Qual­i­ties of Music

The Musi­cal Mind of Albert Ein­stein: Great Physi­cist, Ama­teur Vio­lin­ist and Devo­tee of Mozart

The Secret Link Between Jazz and Physics: How Ein­stein & Coltrane Shared Impro­vi­sa­tion and Intu­ition in Com­mon

Josh Jones is a writer and musi­cian based in Durham, NC. Fol­low him at @jdmagness